 If you live in a culture that values cakes, you know that there are times when not all the cake is eaten. Sometimes, when the cake is being eaten by just one or two individuals of modest appetite (rather than being entirely consumed at some huge family gathering), some of it has to be stored for 'later.' With few exceptions, round cakes are cut into sectors/wedges and, whether stored in the refrigerator or some container at room temperature, the cut surfaces dry out!
If you live in a culture that values cakes, you know that there are times when not all the cake is eaten. Sometimes, when the cake is being eaten by just one or two individuals of modest appetite (rather than being entirely consumed at some huge family gathering), some of it has to be stored for 'later.' With few exceptions, round cakes are cut into sectors/wedges and, whether stored in the refrigerator or some container at room temperature, the cut surfaces dry out!
This problem obviously bothered a very famous scientist, Francis Galton. It bothered him sufficiently that he calculated the geometry and area of round cakes and sent a letter off to that premier science magazine, Nature. His letter was published on 20 December 1906!
What was his recommendation? It was to cut cakes differently.
This is the text of his letter:
Christmas suggests cakes, and the wish on my part [is] to describe a method of cutting them that I have recently devised to my own amusement and satisfaction.
The problem to be solved was, "given a round tea-cake of some 5 inches across, and two persons of moderate appetite to eat it, in what way should it be cut so as to leave a minimum of exposed surface to become dry?"
The ordinary method of cutting out a wedge is very faulty in this respect. The results to be aimed at are so to cut the cake that the remaining portions shall fit together.
Consequently the chords (or the arcs) of the circumferences of these portions must be equal.
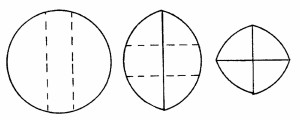 The direction of the first two vertical planes of section is unimportant; they may be parallel, as in the first figure, or they may enclose a wedge.
The direction of the first two vertical planes of section is unimportant; they may be parallel, as in the first figure, or they may enclose a wedge.
The cuts shown on the figures represent those made with the intention of letting the cake last for three days, each successive operation having removed about one-third of the area of the original disc.
A common india-rubber band embraces the whole and keeps its segments together.
Now you know!
By the way, for more advanced mathematicians, an interesting exercise would be to calculate the amount of cake that has to be removed in each case, so as to consume one third of the cake on three consecutive days. Imagine that you have a cake with a radius if 200 mm and then provide precise instructions concerning where to place each cut. Can you suggest a geometric way of locating the cuts so that you don't have to measure?









